Insight article
Revealing the complex subsurface: The spectral-element FWI advantage
22 May 2025
Written by: Lorenzo CasasantaIn an era where the complexity of geophysical targets is ever-increasing, the demand for seismic modelling and inversion technologies that can meet modern exploration challenges has never been greater. The Spectral-Element Method (SEM) is rapidly emerging as a game-changing alternative to traditional Finite-Difference (FD) approaches, offering a powerful combination of numerical accuracy, geometric flexibility, and computational efficiency. In this article, we explore the technological underpinnings of SEM, highlight key findings from field trials, and look ahead to its transformative potential for the geoscience community.
Rethinking the foundations: From FD to SEM
For decades, FD methods have formed the backbone of seismic modelling thanks to their computational efficiency on structured grids. However, their limitations become apparent in scenarios involving complex interfaces, strong material heterogeneities, and challenging topographic conditions. SEM addresses these challenges head-on by combining high-order numerical precision with the flexibility of unstructured meshes. This allows for more accurate modelling of real-world geological settings where Cartesian grid-based methods struggle.
By leveraging high-order polynomial basis functions and the Galerkin method principles, SEM can model seismic wave propagation with remarkable fidelity. One of its most impactful advantages is the natural enforcement of boundary conditions across fluid-solid interfaces, making it ideal for elastic simulations in complex, coupled domains such as those encountered in ocean-bottom node (OBN) surveys and shallow water environments.
Built for complexity: Features that set SEM apart
- Unstructured Mesh Support: Unlike FD methods that are constrained to rectilinear grids, SEM uses unstructured meshes to conform to intricate subsurface geometries, highly heterogeneous material properties and complex boundary interfaces such as topography, bathymetry and geo-bodies.
- High-Order Accuracy: Polynomial basis functions of higher order enable superior wavefield representation, reducing phase and amplitude distortion from low to high frequency bands.
- Direct Access to Physical Quantities: SEM allows for precise computation of displacement, velocity, strain, and stress without interpolation—critical for advanced applications such as distributed acoustic sensing (DAS), carbon capture and storage (CCS) monitoring, and near-surface site characterization.
- Elastic and Anisotropic Media: Advanced numerical formulations enable accurate simulation in vertically and tilted transversely isotropic (VTI/TTI) elastic media, supporting a wide range of exploration and monitoring scenarios.
Accelerated by modern computing
SEM’s compatibility with GPU-accelerated hardware is a significant enabler for its scalability. Its diagonal mass matrix structure ensures efficient computations across parallel architectures. Advanced meshing techniques, including local adaptive refinement and aperture mesh cut-outs, further reduce computational overhead without sacrificing model fidelity. In areas with low-velocity sediments, SEM's local time-stepping can provide up to an order of magnitude speed-up by decoupling the global time step from fine-mesh regions.
Smarter inversions: SEM-driven FWI with optimization and preconditioning
Incorporating non-linear optimization techniques such as Trust-Region Quasi-Newton L-BFGS and a novel anisotropic diffusion-based preconditioner, SEM-based full-waveform inversion (FWI) achieves faster and geologically plausible convergence. These tools are natively compatible with SEM’s unstructured mesh format, aligning model updates with subsurface structures in a physically meaningful way.
Field-proven performance: Offshore Western Australia case study
To validate the practical benefits of SEM, a field streamer dataset from offshore Western Australia was modelled and inverted using both FD and SEM-based workflows. The seabed in this region features dramatic bathymetric variations, making it an ideal test case for topographic handling.
Key findings from the comparison include:
Superior Waveform Alignment: SEM simulations showed cleaner phase alignment with observed data, especially near complex topographic features.
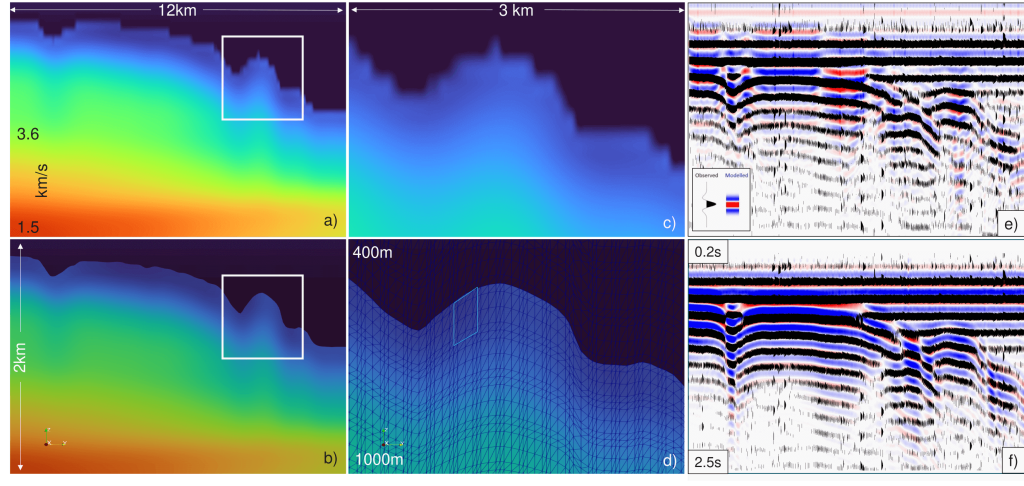
Figure 1: Subsurface velocity models used for FD (e) and SEM (f) forward modelling calculations are shown. Model (a) is discretized using a conventional rectilinear grid with 60 m point spacing, while Model (b) is discretized using an unstructured mesh with quadrilateral elements of polynomial order 4. A zoomed-in view (white square) of the seabed topography highlights the FD (c) and SEM (d) models, with the SEM model showing the deformed quadrilateral elements. Near-channel waveforms for FD (e) and SEM (f) are computed at 550 shot locations.
Improved FWI Model Updates: While both FD and SEM produced broadly similar updates, SEM demonstrated greater lateral continuity and resolution.
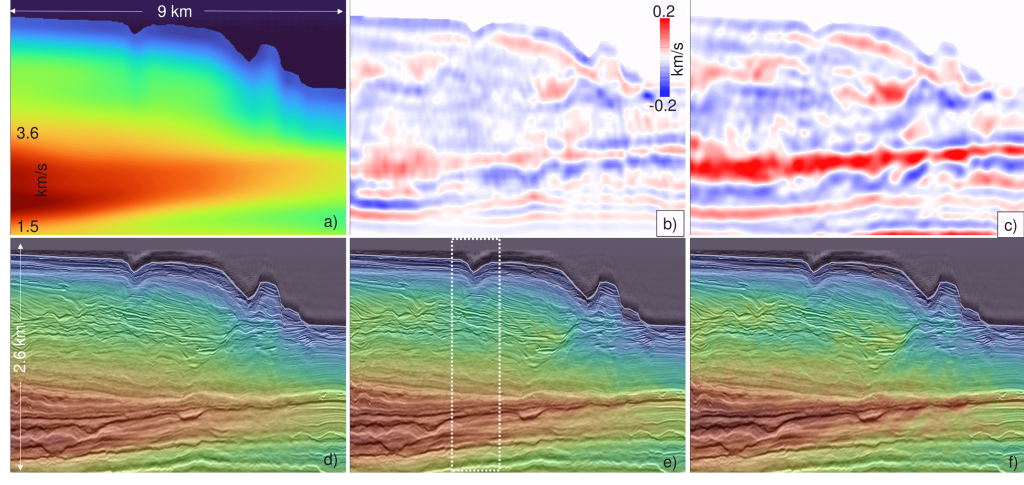
Figure 2: Initial velocity model for the 5–12 Hz acoustic full-waveform inversion. Panels (b) and (c) show the cumulative velocity updates for FD and SEM, respectively. Panel (d) displays the initial velocity model overlaid with the Kirchhoff depth-migrated seismic data, while panels (e) and (f) present the final FD and SEM velocity models, respectively, with migrated seismic as the background. The white dotted square highlights a region where SEM imaging is considered superior to FD imaging.
Enhanced Migration Results: Kirchhoff depth migrations using SEM-updated velocity models revealed clearer subsurface features, particularly beneath canyons, where FD methods introduced artifacts due to poor discretization.
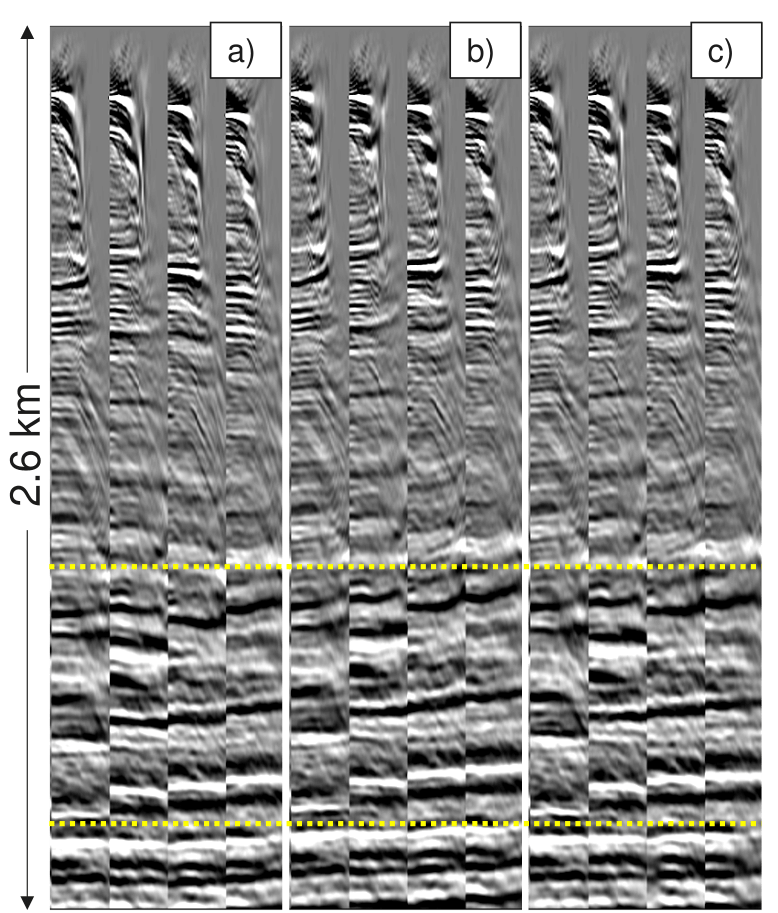
Figure 3: Kirchhoff Depth Migration Offset Gathers obtained with the initial (a) and final FD (b) and SEM (c) velocity models from Figure 2. The gathers are from the area highlighted by the white squared dotted rectangle. The maximum imaged offset is 3km.
Looking ahead: A platform for the future
SEM’s ability to precisely model complex subsurface conditions position it as a foundational technology for future-facing geophysical challenges. Its flexibility and precision make it uniquely suited for applications extending beyond traditional oil and gas exploration, including carbon storage integrity monitoring and fibre-optic DAS imaging
As hardware architectures and numerical algorithms continue to advance, SEM’s efficiency and scope will only grow. For our clients, this means access to higher-fidelity subsurface insights, reduced modelling uncertainty, and more confident decision-making in complex geologic environments.
Final thoughts
By overcoming the fundamental limitations of FD methods, SEM opens new doors for geophysicists tackling some of the most complex challenges in the subsurface. From improved modelling fidelity to faster, more robust inversion results, SEM is poised to become the seismic engine behind the next generation of exploration and monitoring technologies.
Acknowledgements: We thank Shearwater, Mondaic AG, and Geoscience Australia for their support and the datasets that enabled this work.
Related articles
Locking into Harmony: how bubble science is changing the game
Science and seismic innovation for smarter and faster energy exploration
